Loads In Buildings:
In Building construction during design of RCC/Steel
structures the frame systems are designed to withstand the loads which the
building will serve for its design life. In this post i will illustrate the
basics of the design loads considered while designing of structures & the
basic mathematics involved in their calculation.
Types of building loads:
In a typical residential building as discussed below
the following given loads are present;
1. Dead Load – Under this category all the load of the
dead or non-moving/stationary/fixed elements of the building are considered
such as dead weight of walls, weight of roof/floor finishes, self weight of
structural members such as; beams, coloumns, Footings & RCC slabs etc. The
calculation of live loads has to be done by taking properties of the material
& the dimensions of the element considered.
2. Live Load – In live load category the moving loads
such as due to human use or furniture or any other mechanical equipment are
considered. For all general categories live loads are defined in Indian Code IS
875 Part-3 rest if any shall be calculated as per the requirement.
3. Dynamic Load – Apart from dead & live loads a building structure is also subjected to application of dynamic load. Dynamic loads are the loads in which the value & nature of application of force is not constant throughout & is subjected to changes as per the conditions governing the forces. Forces due to wind, earthquake, traffic or heavy machinery (such as blowers or pumps) falls under this category.
Dead Loads:
1.
Self weight- It is the weight of the frame or
the individual weight of the structural elements such as Beams, Columns &
Slabs. In computer programs such as STAAD Pro inbuilt capability is there which
allows the program to calculate the self weight of the elements automatically
in accordance with the shape, size & member dimensions.
Example: Below given are the examples for manual calculation of
self-weight of the structural elements.
a.
Beam: Let it be of any shape
Rectangular/square/tee/trapezoid anything for calculation of weight use the
given formula;
Weight of member = cross section area of
member x length of member x RCC density
For a 0.3 m wide 0.45 m deep beam
section of 5 m clear length & material density = 25 kn/m3 (for
RCC), the weight will be;
Weight of beam = (0.3 x 0.45) x 5 x 25 = 16.875 Kn
The above calculated weight of 16.875 Kn is the total weight which can
be further converted into Uniformly Distributed Load (UDL) by dividing the
total weight by member length.
UDL = 16.875/5 = 3.375 Kn/m
b.
Column: Same as explained above the self-weight
of a column can be calculated only the terminology of member length will be
changed to member height & the weight of column will be calculated as point
load only its conversion in UDL is not required.
c.
Slab: RCC slabs,
the weight of roof slabs is applied as uniform pressure in Kn/m2.
For analysis purpose it is we consider a 1 m x 1 m square section &
calculate the volume of the RCC & then the same is multiplied with the
density for derivation of pressure in kn/m2.
Weight of slab = (1 x 1 x slab thickness) x RCC
density
In the above formula as (1 x 1)
doesn’t effects the calculation thus it can be further simplified as;
Weight of slab = slab thickness x RCC density
For 0.15 m thick slab the calculation
will be as follows;
Weight of slab = 0.15 x 25 = 3.75 Kn/m2
In the above calculation of RCC slab
weight further additional load due to floor finishes are to be included
generally for stone/cement floorings 0.75 kn/m2 to 1.5 kn/m2
is considered.
Distribution of slab load on
supporting beams:
Depending upon the arrangement of
beams (square or rectangular) triangular or trapezoidal shape distribution is
carried out. For example (refer fig-1 below) in case of a rectangular slab of 6
m x 4 m the longer side beams spanning between A-B & D-C will carry the
load of corresponding trapezoidal portion whereas the shorter span beams
spanning between A-D & B-C will support weight of roof slab coming from
corresponding triangular region.
Load on 6 m span = area of trapezoid x
thickness of slab x density
Load on 6 m span = 8 x 0.15 x 25 = 30 Kn
= 30 / member length = 30/6 = 5 Kn/m
The above
calculated load of 30 Kn can be further converted in UDL of 5 kn/m by dividing
it by member length as shown above.
Load on 4 m span = area of triangle x
thickness of slab x density
Load on 4 m span = 4 x 0.15 x 25 = 15 Kn = 15 / member length = 15/4 = 3.75 Kn/m
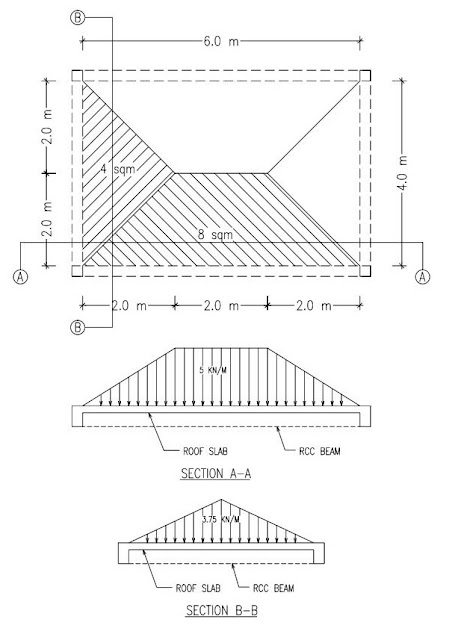 |
| Fig-1 Load distribution of slabs on supporting beam members/load bearing walls |
Above discussed was the case of
rectangular slab whereas in the case of square slab the slab plan will be
divided in 4 nos. of equal triangles & the load for the same will be
transferred to the corresponding beam members.
d.
Walls: Generally in building construction
brick walls of single brick (0.115 m thick) & double brick (0.230 m thick)
are used, the load of brick walls is calculated as follows;
Weight of wall (In KN/m) = Height of wall x
thickness of wall x density of brick/stone masonry
For 0.23 m thick wall of 3.2 m clear
height the load will be;
Weight of wall (In KN/m) = 3.2 x 0.230 x 22 = 16.192 Kn/m
The above calculated load of 16.192
Kn/m will be applicable in the form of UDL on the beam members supporting the
brick wall, in above calculation brick wall density considered is 22 Kn/m3.
Live Loads:
Live loads or imposed loads as per building type & occupancy
classification shall be provided as per Indian Code IS 875 Part-2 in table-1.
Dynamic Loads:
Mainly, the RCC buildings are subjected to two dynamic forces;
- Wind Force: To be calculated in line with the provisions of IS 875 (Part-3).
- Seismic/Earthquake Force: To be calculated in line with the provisions of IS 1893: 2016.
methodology for calculation of wind forces & earthquake forces will be discussed in separate post, keep following.
Hope above given explanation helps in understanding the basics for determination of dead & live loads as per Indian Code.
Regards
Alok Dixit











